-
ANOVA 예제 1, 2(정규성, 등분산성 검정, 사후 검정) 귀무 vs 대립Python 데이터 분석 2022. 11. 9. 17:28
ANOVA 예제 1
작성자 코드
# [ANOVA 예제 1] # 빵을 기름에 튀길 때 네 가지 기름의 종류에 따라 빵에 흡수된 기름의 양을 측정하였다. # 기름의 종류에 따라 흡수하는 기름의 평균에 차이가 존재하는지를 분산분석을 통해 알아보자. # 조건 : NaN이 들어 있는 행은 해당 칼럼의 평균값으로 대체하여 사용한다. import numpy as np import scipy.stats as stats import pandas as pd import matplotlib.pyplot as plt # 귀무 : 기름의 종류에 따라 흡수하는 기름의 평균에 차이는 없다. # 귀무 : 기름의 종류에 따라 흡수하는 기름의 평균에 차이는 있다. kind = [1, 2, 3, 4, 2, 1, 3, 4, 2, 1, 2, 3, 4, 1, 2, 1, 1, 3, 4, 2] quantity = [64, 72, 68, 77, 56, 0, 95, 78, 55, 91, 63, 49, 70, 80, 90, 33, 44, 55, 66, 77] df1 = pd.DataFrame(kind) df2 = pd.DataFrame(quantity) df2.iloc[5, 0] = np.nan df = pd.concat([df1, df2], axis = 1) df.columns = ['기름종류', '흡수량'] df['흡수량'] = df['흡수량'].fillna(df['흡수량'].mean()) df = df.astype('int') print(df) result = df[['기름종류', '흡수량']] m1 = result[result['기름종류'] == 1] m2 = result[result['기름종류'] == 2] m3 = result[result['기름종류'] == 3] m4 = result[result['기름종류'] == 4] gr1 = m1['흡수량'] gr2 = m2['흡수량'] gr3 = m3['흡수량'] gr4 = m4['흡수량'] # print(gr1[:3]) # print(gr2[:3]) # print(gr3[:3]) # print(gr4[:3]) print(np.mean(gr1), ' ', np.mean(gr2), ' ', np.mean(gr3), ' ', np.mean(gr4)) # 63.166666666666664 vs 68.83333333333333 vs 66.75 vs 72.75 # 한 개의 표본이 같은 분포를 따르는지 정규성 확인 print(stats.shapiro(gr1).pvalue) # 0.86710 > 0.05 이르로 정규성 만족 print(stats.shapiro(gr2).pvalue) # 0.59239 > 0.05 이르로 정규성 만족 print(stats.shapiro(gr3).pvalue) # 0.48601 > 0.05 이르로 정규성 만족 print(stats.shapiro(gr4).pvalue) # 0.41621 > 0.05 이르로 정규성 만족 print() # 두 개의 표본이 같은 분포를 따르는지 정규성 확인 print(stats.ks_2samp(gr1, gr2).pvalue) # 0.9307 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(gr1, gr3).pvalue) # 0.9238 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(gr1, gr4).pvalue) # 0.5523 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(gr2, gr3).pvalue) # 0.9238 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(gr2, gr4).pvalue) # 0.5523 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(gr3, gr4).pvalue) # 0.7714 > 0.05 이므로 정규성 만족 print() # 등분산성 : 만족하지 않으면 welchi_anova test 사용 print(stats.bartlett(gr1, gr2, gr3, gr4).pvalue) # 0.1938 > 0.05 이므로 등분산성 만족 # 데이터의 퍼짐 정도 시각화 plt.boxplot([gr1, gr2, gr3, gr4], showmeans = True) plt.show() # 일원분산분석 방법 : f_oneway() f_sta, pvalue = stats.f_oneway(gr1, gr2, gr3, gr4) print('f통계량 : ', f_sta) # 0.27241 print('유의확률 : ', pvalue) # 0.84438 > 0.05이므로 귀무 채택. # 기름의 종류에 따라 흡수하는 기름의 평균에 차이는 없다. # 사후검정 from statsmodels.stats.multicomp import pairwise_tukeyhsd turkeyResult = pairwise_tukeyhsd(endog = df.흡수량, groups = df.기름종류) print(turkeyResult) # 차이가 없으면 reject가 False가 나오고, 차이가 크면 True가 나온다. # 시각화 turkeyResult.plot_simultaneous(xlabel = 'mean', ylabel = 'group') plt.show() <console> 기름종류 흡수량 0 1 64 1 2 72 2 3 68 3 4 77 4 2 56 5 1 67 6 3 95 7 4 78 8 2 55 9 1 91 10 2 63 11 3 49 12 4 70 13 1 80 14 2 90 15 1 33 16 1 44 17 3 55 18 4 66 19 2 77 63.166666666666664 68.83333333333333 66.75 72.75 0.8671070337295532 0.5923936367034912 0.4860108494758606 0.41621729731559753 0.9307359307359307 0.9238095238095239 0.5523809523809524 0.9238095238095239 0.5523809523809524 0.7714285714285716 0.19384085898800654 f통계량 : 0.27241333670240286 유의확률 : 0.8443828299994541 Multiple Comparison of Means - Tukey HSD, FWER=0.05 ===================================================== group1 group2 meandiff p-adj lower upper reject ----------------------------------------------------- 1 2 5.6667 0.9373 -22.3934 33.7267 False 1 3 3.5833 0.9875 -27.7887 34.9554 False 1 4 9.5833 0.8181 -21.7887 40.9554 False 2 3 -2.0833 0.9975 -33.4554 29.2887 False 2 4 3.9167 0.9838 -27.4554 35.2887 False 3 4 6.0 0.958 -28.3664 40.3664 False -----------------------------------------------------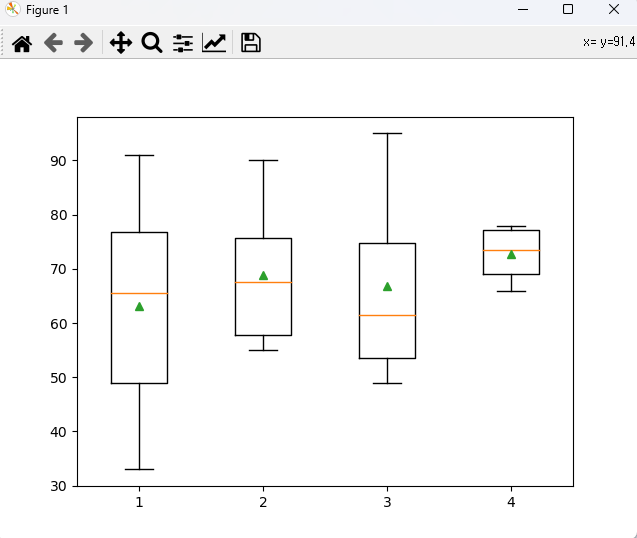
문제 1번 데이터의 퍼짐 정도 시각화 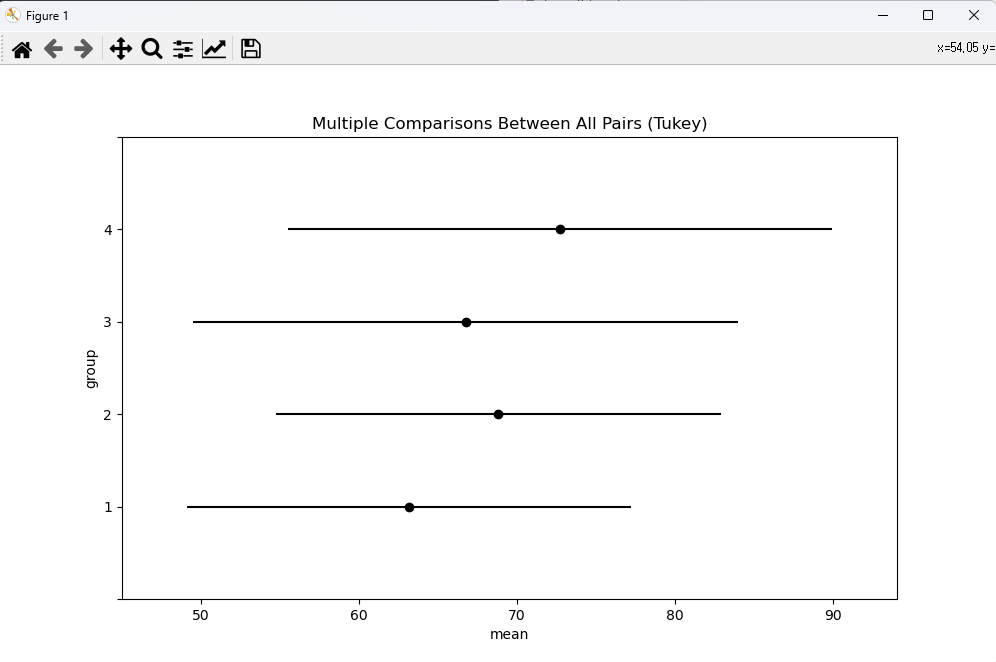
문제 1번 사후검증 시각화 다른 방법 코드
import pandas as pd import scipy.stats as stats from statsmodels.formula.api import ols from statsmodels.stats.anova import anova_lm import matplotlib.pyplot as plt import numpy as np import urllib.request # [ANOVA 예제 1] # 빵을 기름에 튀길 때 네 가지 기름의 종류에 따라 빵에 흡수된 기름의 양을 측정하였다. # 기름의 종류에 따라 흡수하는 기름의 평균에 차이가 존재하는지를 분산분석을 통해 알아보자. # 조건 : NaN이 들어 있는 행은 해당 칼럼의 평균값으로 대체하여 사용한다. # 귀무 : 빵을 기름에 튀길 때 기름의 종류에 따라 흡수하는 기름의 평균에 차이가 없다. # 대립 : 빵을 기름에 튀길 때 기름의 종류에 따라 흡수하는 기름의 평균에 차이가 있다. # kind = [1,2,3,4,2,1,3,4,2,1,2,3,4,1,2,1,1,3,4,2] # quantity = [64,72,68,77,56,NaN,95,78,55,91,63,49,70,80,90,33,44,55,66,77] data=pd.read_csv("../testdata/bbang.csv",delimiter=' ') print(data.head(6)) print(data.shape) # (20, 2) data = data.fillna({'quantity':data['quantity'].mean()}) data.isnull().sum() print(data) print(data.describe()) result = data[['kind', 'quantity']] k1 = result[result['kind']== 1] k2 = result[result['kind']== 2] k3 = result[result['kind']== 3] k4 = result[result['kind']== 4] quan1 = k1['quantity'] quan2 = k2['quantity'] quan3 = k3['quantity'] quan4 = k4['quantity'] print(quan1[:6]) print(quan2[:6]) print(quan3[:6]) print(quan4[:6]) print('평균 : ', np.mean(quan1), ' ', np.mean(quan2), ' ', np.mean(quan3), ' ', np.mean(quan4)) # 정규성 확인 # 한 개의 표본이 같은 분포를 따르는지 확인 print(stats.shapiro(quan1).pvalue) # 0.86804 > 0.05 크므로 만족 print(stats.shapiro(quan2).pvalue) # 0.59239 print(stats.shapiro(quan3).pvalue) # 0.48601 print(stats.shapiro(quan4).pvalue) # 0.41621 # 두 개의 표본이 같은 분포를 따르는지 확인 print(stats.ks_2samp(quan1, quan2).pvalue) # 0.93073 > 0.05 크므로 만족 print(stats.ks_2samp(quan1, quan3).pvalue) print(stats.ks_2samp(quan1, quan4).pvalue) print(stats.ks_2samp(quan2, quan3).pvalue) print(stats.ks_2samp(quan2, quan4).pvalue) print(stats.ks_2samp(quan3, quan4).pvalue) print() # 등분산성 확인 print(stats.levene(quan1, quan2, quan3, quan4).pvalue) # 0.32689 > 0.05 크므로 만족 # anova 진행 import statsmodels.api as sm reg = ols('kind ~ quantity', data=data).fit() table =sm.stats.anova_lm(reg, type=2) print(table) # df sum_sq mean_sq F PR(>F) # quantity 1.0 0.85241 0.852410 0.657172 0.428149 # Residual 18.0 23.34759 1.297088 NaN NaN #================================================================================================== # 해석 : p-value = 0.428149 > 0.05 크므로 귀무채택. 빵을 기름에 튀길 때 기름의 종류에 따라 흡수하는 기름의 평균에 차이가 없다. #================================================================================================== # 사후검증 # post hoc test from statsmodels.stats.multicomp import pairwise_tukeyhsd tukeyResult = pairwise_tukeyhsd(endog= data.kind, groups=data.quantity) # 알파값은 기본적으로 0.05다 print(tukeyResult) <console> kind quantity 0 1 64.0 1 2 72.0 2 3 68.0 3 4 77.0 4 2 56.0 5 1 NaN (20, 2) kind quantity 0 1 64.000000 1 2 72.000000 2 3 68.000000 3 4 77.000000 4 2 56.000000 5 1 67.526316 6 3 95.000000 7 4 78.000000 8 2 55.000000 9 1 91.000000 10 2 63.000000 11 3 49.000000 12 4 70.000000 13 1 80.000000 14 2 90.000000 15 1 33.000000 16 1 44.000000 17 3 55.000000 18 4 66.000000 19 2 77.000000 kind quantity count 20.000000 20.000000 mean 2.300000 67.526316 std 1.128576 15.981464 min 1.000000 33.000000 25% 1.000000 55.750000 50% 2.000000 67.763158 75% 3.000000 77.250000 max 4.000000 95.000000 0 64.000000 5 67.526316 9 91.000000 13 80.000000 15 33.000000 16 44.000000 Name: quantity, dtype: float64 1 72.0 4 56.0 8 55.0 10 63.0 14 90.0 19 77.0 Name: quantity, dtype: float64 2 68.0 6 95.0 11 49.0 17 55.0 Name: quantity, dtype: float64 3 77.0 7 78.0 12 70.0 18 66.0 Name: quantity, dtype: float64 평균 : 63.25438596491228 68.83333333333333 66.75 72.75 0.8680403232574463 0.5923936367034912 0.4860108494758606 0.41621729731559753 0.9307359307359307 0.9238095238095239 0.5523809523809524 0.9238095238095239 0.5523809523809524 0.7714285714285716 0.3268969935062273 df sum_sq mean_sq F PR(>F) quantity 1.0 0.85241 0.852410 0.657172 0.428149 Residual 18.0 23.34759 1.297088 NaN NaN Multiple Comparison of Means - Tukey HSD, FWER=0.05ANOVA 예제 2
# [ANOVA 예제 2] # DB에 저장된 buser와 jikwon 테이블을 이용하여 총무부, 영업부, 전산부, 관리부 직원의 연봉의 평균에 차이가 있는지 검정하시오. # 만약에 연봉이 없는 직원이 있다면 작업에서 제외한다. import MySQLdb import pickle # 귀무 : 총무부, 영업부, 전산부, 관리부 직원의 연봉의 평균에 차이는 없다. # 대립 : 총무부, 영업부, 전산부, 관리부 직원의 연봉의 평균에 차이는 있다. with open('mydb.dat', mode='rb') as obj: config = pickle.load(obj) try: conn = MySQLdb.connect(**config) cursor = conn.cursor() sql = """ select buser_name, jikwon_pay from jikwon JOIN buser ON buser_num = buser_no """ cursor.execute(sql) # datas = cursor.fetchall() # 이 방법도 있다. datas = pd.read_sql(sql, conn) df = pd.DataFrame(datas) df.columns = '부서명', '연봉' print(df.head(4)) # print("부서멸 연봉의 합 : ", df.groupby(['부서명'])['연봉'].sum()) print("부서별 연봉의 합 : ", df.groupby(['부서명'])['연봉'].mean()) # 6262 vs 4908 vs 5328 vs 5414 평균 차이? a = df[df['부서명'] == '총무부'] a_pay_mean = a.loc[:,'연봉'] print(a_pay_mean) b = df[df['부서명'] == '영업부'] b_pay_mean = b.loc[:,'연봉'] print(b_pay_mean) c = df[df['부서명'] == '전산부'] c_pay_mean = c.loc[:,'연봉'] print(c_pay_mean) d = df[df['부서명'] == '관리부'] d_pay_mean = d.loc[:,'연봉'] print(d_pay_mean) # 한 개의 표본이 같은 분포를 따르는지 정규성 확인 print(stats.shapiro(a_pay_mean)) # pvalue=0.02604 < 0.05 이므로 정규성 불만족 print(stats.shapiro(b_pay_mean)) # pvalue=0.02560 < 0.05 이므로 정규성 불만족 print(stats.shapiro(c_pay_mean)) # pvalue=0.41940 < 0.05 이므로 정규성 만족 print(stats.shapiro(d_pay_mean)) # pvalue=0.90780 < 0.05 이므로 정규성 만족 print() # 두 개의 표본이 같은 분포를 따르는지 정규성 확인 print(stats.ks_2samp(a_pay_mean, b_pay_mean).pvalue) # 0.33577 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(a_pay_mean, c_pay_mean).pvalue) # 0.57517 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(a_pay_mean, d_pay_mean).pvalue) # 0.53636 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(b_pay_mean, c_pay_mean).pvalue) # 0.33577 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(b_pay_mean, d_pay_mean).pvalue) # 0.64065 > 0.05 이므로 정규성 만족 print(stats.ks_2samp(c_pay_mean, d_pay_mean).pvalue) # 0.53636 > 0.05 이므로 정규성 만족 print() # 등분산성 : 만족하지 않으면 welchi_anova test 사용 print(stats.bartlett(a_pay_mean, b_pay_mean, c_pay_mean, d_pay_mean).pvalue) # 0.62909 > 0.05 이므로 등분산성 만족 # 데이터의 퍼짐 정도 시각화 plt.boxplot([a_pay_mean, b_pay_mean, c_pay_mean, d_pay_mean], showmeans = True) plt.show() print() # 일원분산분석 방법 : f_oneway() f_sta, pvalue = stats.f_oneway(a_pay_mean, b_pay_mean, c_pay_mean, d_pay_mean) print('f통계량 : ', f_sta) # 0.41244 print('유의확률 : ', pvalue) # 0.74544 > 0.05 이므로 귀무 채택. # 귀무 : 총무부, 영업부, 전산부, 관리부 직원의 연봉의 평균에 차이는 없다. # 사후검정 from statsmodels.stats.multicomp import pairwise_tukeyhsd turkeyResult = pairwise_tukeyhsd(endog = df.연봉, groups = df.부서명) print(turkeyResult) # 차이가 없으면 reject가 False가 나오고, 차이가 크면 True가 나온다. # 시각화 turkeyResult.plot_simultaneous(xlabel = 'mean', ylabel = 'group') plt.show() except Exception as e: print('err :', e) finally: cursor.close() conn.close() <console> 부서명 연봉 0 총무부 9900 1 영업부 8800 2 영업부 7900 3 전산부 4500 부서별 연봉의 합 : 부서명 관리부 6262.500000 영업부 4908.333333 전산부 5328.571429 총무부 5414.285714 Name: 연봉, dtype: float64 0 9900 9 3700 12 4900 16 8000 24 3800 25 3500 28 4100 Name: 연봉, dtype: int64 1 8800 2 7900 4 3000 5 2950 7 7800 14 4000 15 3000 19 2900 20 2950 23 4500 26 5900 27 5200 Name: 연봉, dtype: int64 3 4500 8 5000 10 3900 17 7800 18 5500 22 6600 29 4000 Name: 연봉, dtype: int64 6 8600 11 7200 13 3400 21 5850 Name: 연봉, dtype: int64 ShapiroResult(statistic=0.7803537845611572, pvalue=0.02604489028453827) ShapiroResult(statistic=0.8372057676315308, pvalue=0.02560843899846077) ShapiroResult(statistic=0.9133293628692627, pvalue=0.4194071292877197) ShapiroResult(statistic=0.9809899926185608, pvalue=0.9078023433685303) 0.3357743907279511 0.5751748251748252 0.5363636363636364 0.3357743907279511 0.6406593406593406 0.5363636363636364 0.6290955395410989 f통계량 : 0.41244077160708414 유의확률 : 0.7454421884076983 Multiple Comparison of Means - Tukey HSD, FWER=0.05 =========================================================== group1 group2 meandiff p-adj lower upper reject ----------------------------------------------------------- 관리부 영업부 -1354.1667 0.6937 -4736.5568 2028.2234 False 관리부 전산부 -933.9286 0.897 -4605.9199 2738.0628 False 관리부 총무부 -848.2143 0.9202 -4520.2056 2823.7771 False 영업부 전산부 420.2381 0.9756 -2366.0209 3206.4971 False 영업부 총무부 505.9524 0.9588 -2280.3066 3292.2114 False 전산부 총무부 85.7143 0.9998 -3045.7705 3217.199 False -----------------------------------------------------------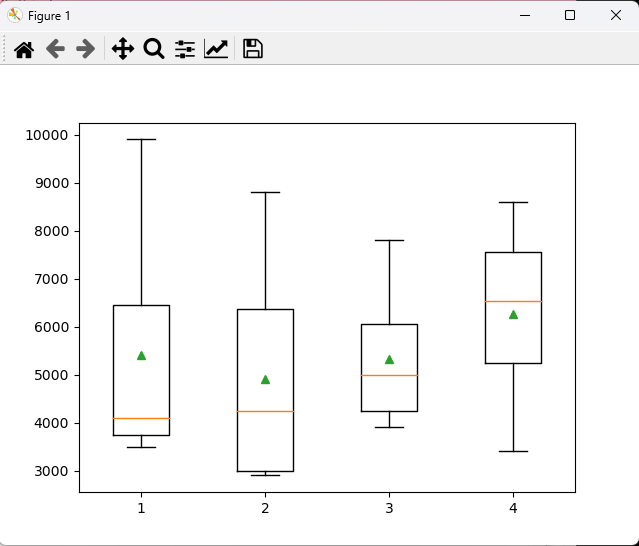
문제 2번 데이터의 퍼짐 정도 시각화 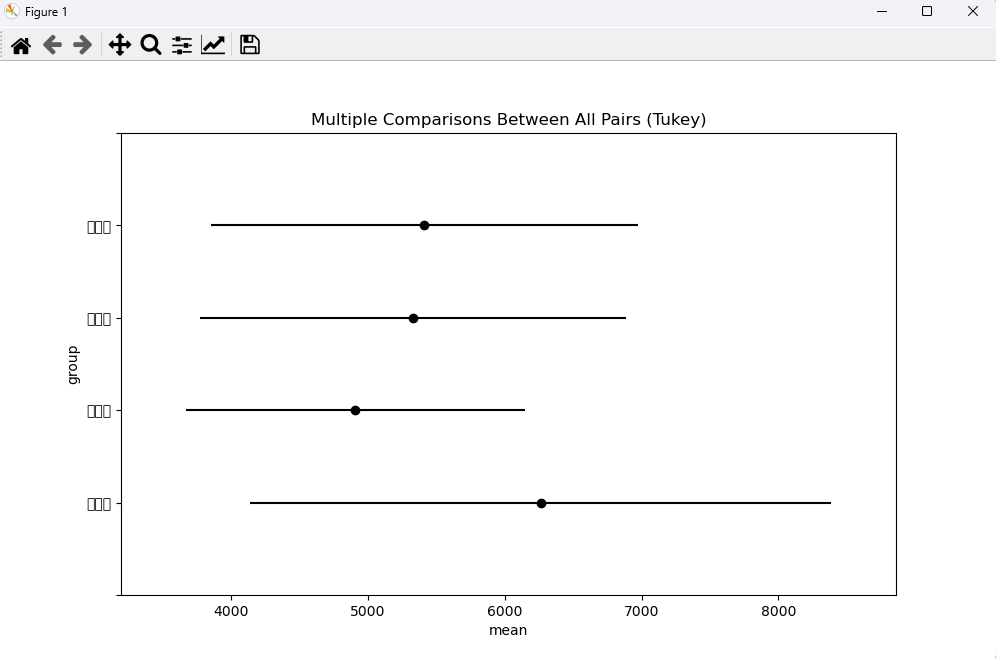
문제 2번 사후검정 시각 'Python 데이터 분석' 카테고리의 다른 글
Python 데이터분석 기초 40 - 추론통계 분석 중 비율(value)검정 (0) 2022.11.10 Python 데이터분석 기초 39 - Two-way ANOVA(이원분산분석) (0) 2022.11.09 Python 데이터분석 기초 38 - 어느 음식점 매출 자료와 날씨 자료를 활용하여 온도(추움, 보통, 더움)에 따른 매출액 평균에 차이를 검정 + 웹 (0) 2022.11.09 Python 데이터분석 기초 37 - 일원분산분석으로 평균차이 검정(웹에서 데이터 가져오기) (0) 2022.11.09 Python 데이터분석 기초 36 - 세 개 이상의 모집단에 대한 가설검정 – 분산분석(ANOVA), 사후검정 (0) 2022.11.09