Python 데이터분석 기초 36 - 세 개 이상의 모집단에 대한 가설검정 – 분산분석(ANOVA), 사후검정

 

세 개 이상의 모집단에 대한 가설검정 – 분산분석
‘분산분석’이라는 용어는 분산이 발생한 과정을 분석하여 요인에 의한 분산과 요인을 통해 나누어진 각 집단 내의 분산으로 나누고 요인에 의한 분산이 의미 있는 크기를 크기를 가지는지를 검정하는 것을 의미한다.
세 집단 이상의 평균비교에서는 독립인 두 집단의 평균 비교를 반복하여 실시할 경우에 제1종 오류가 증가하게 되어 문제가 발생한다.
이를 해결하기 위해 Fisher가 개발한 분산분석(ANOVA, ANalysis Of Variance, F분포를 이용)을 이용하게 된다.
* 서로 독립인 세 집단의 평균 차이 검정

 

ANOVA = 하나의 요인에 집단이 3개 이상 있을 때 사용(평균의 차이를 검정할 때)

  

# 세 개 이상의 모집단에 대한 가설검정 – 분산분석
# ‘분산분석’이라는 용어는 분산이 발생한 과정을 분석하여 요인에 의한 분산과 요인을 통해 나누어진 각 집단 내의 분산으로 나누고 요인
# 에 의한 분산이 의미 있는 크기를 크기를 가지는지를 검정하는 것을 의미한다.
# 세 집단 이상의 평균비교에서는 독립인 두 집단의 평균 비교를 반복하여 실시할 경우에 제1종 오류가 증가하게 되어 문제가 발생한다.
# 이를 해결하기 위해 Fisher가 개발한 분산분석(ANOVA, ANalysis Of Variance, F분포를 이용)을 이용하게 된다.
# * 서로 독립인 세 집단의 평균 차이 검정

# 실습) 세 가지 교육방법을 적용하여 1개월 동안 교육받은 교육생 80명을 대상으로 실기시험을 실시. three_sample.csv'

import pandas as pd
import scipy.stats as stats
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
import numpy as np

# 교육방법이 한 개의 요인. 요인이 3가지 방법으로 구분 - 세 개의 집단
# 귀무 : 세 가지 교육방법에 따른 시험점수에 차이가 없다.
# 대립 : 세 가지 교육방법에 따른 시험점수에 차이가 있다.

data = pd.read_csv('../testdata/three_sample.csv')
print(data.head(3))
print(data.shape)      # 행렬 호출
print(data.describe()) # 통계 호출

# plt.boxplot(data.score)
# plt.hist(data.score)
# plt.show()

data = data.query('score <= 100')  # 100을 넘어가는 이상치 제거
print(data.shape) # (78, 4)

result = data[['method', 'score']]
m1 = result[result['method'] == 1]
m2 = result[result['method'] == 2]
m3 = result[result['method'] == 3]

score1 = m1['score']
score2 = m2['score']
score3 = m3['score']
print(score1[:3])
print(score2[:3])
print(score3[:3]) # 3행까지 출력

print('평균 :', np.mean(score1), ' ', np.mean(score2), ' ', np.mean(score3))
# 평균 : 67.384   68.357   68.875

# 정규성을 만족하면 anova, 만족하지 않으면 kruskal-wallis test 사용
# 한 개의 표본이 같은 분포를 따르는지 정규성 확인
print(stats.shapiro(score1).pvalue)  # 0.17467 > 0.05 이므로 정규성 만족
print(stats.shapiro(score2).pvalue)  # 0.33189 > 0.05 이므로 정규성 만족
print(stats.shapiro(score3).pvalue)  # 0.11558 > 0.05 이므로 정규성 만족

# 두 개의 표본이 같은 분포를 따르는지 정규성 확인
print(stats.ks_2samp(score1, score2).pvalue)  # 0.30968 > 0.05 이므로 정규성 만족
print(stats.ks_2samp(score2, score3).pvalue)  # 0.77240 > 0.05 이므로 정규성 만족
print(stats.ks_2samp(score1, score3).pvalue)  # 0.71620 > 0.05 이므로 정규성 만족

print()
# 등분산성 : 만족하지 않으면 welchi_anova test 사용
print(stats.levene(score1, score2, score3).pvalue)   # 0.11322 > 0.05 이므로 등분산성 만족
print(stats.fligner(score1, score2, score3).pvalue)  # 0.10847 > 0.05 이므로 등분산성 만족
print(stats.bartlett(score1, score2, score3).pvalue) # 0.15251 > 0.05 이므로 등분산성 만족
# 참고 : 등분산성을 만족하지 않는 경우 대안 : 추천
# 데이터를 정규화, 표준화, 자연 log를 붙이는 방법

print('교육방법별 건수 : 교차표')
data2 = pd.crosstab(index = data['method'], columns = 'count')
data2.index = ['방법1', '방법2', '방법3']
print(data2)

print('교육방법별 만족여부 건수 : 교차표')
data3 = pd.crosstab(data.method, data.survey)
data3.index = ['방법1', '방법2', '방법3']
data3.columns = ['만족', '불만족']
print(data3)

# anova 진행
import statsmodels.api as sm

# 독립변수 : 1, 종속변수 : 1
reg = ols('score ~ method', data = data).fit()   # fit함수는 학습을 하는 함수이다.
table = sm.stats.anova_lm(reg, typ=1)
print(table) # 분산 분석표 출력
# 해석 : p-value 0.727597 > 0.05 이므로 귀무 채택.
# 세 가지 교육방법에 따른 시험점수에 차이가 없다.

# ------------------
print('---------')
# 독립변수 : 2, 종속변수 : 1
reg2 = ols('score ~ C(method + survey)', data = data).fit()   # fit함수는 학습을 하는 함수이다.
table2 = sm.stats.anova_lm(reg2, typ=2)
print(table2) # 분산 분석표 출력
# ------------------

print('사후검정 : 그룹 전체의 평균에 차이여부를 알려주나, 각 그룹 사이에 평균의 차이는 알려주지 않는다. 그래서 사후검정을 수행한다.')
# post hoc test
from statsmodels.stats.multicomp import pairwise_tukeyhsd
turkeyResult = pairwise_tukeyhsd(endog = data.score, groups = data.method)
print(turkeyResult)  # 차이가 없으면 reject가 False가 나오고, 차이가 크면 True가 나온다.

# 시각화
turkeyResult.plot_simultaneous(xlabel = 'mean', ylabel = 'group')
plt.show()


<console>
   no  method  survey  score
0   1       1       1     72
1   2       3       1     87
2   3       2       1     78
(80, 4)
            no     method     survey       score
count  80.0000  80.000000  80.000000   80.000000
mean   40.5000   1.962500   0.650000   78.212500
std    23.2379   0.802587   0.479979   64.886404
min     1.0000   1.000000   0.000000   33.000000
25%    20.7500   1.000000   0.000000   58.000000
50%    40.5000   2.000000   1.000000   65.000000
75%    60.2500   3.000000   1.000000   79.500000
max    80.0000   3.000000   1.000000  500.000000
(78, 4)
0     72
3     54
6    100
Name: score, dtype: int64
2     78
4     84
14    59
Name: score, dtype: int64
1    87
5    44
8    58
Name: score, dtype: int64
평균 : 67.38461538461539   68.35714285714286   68.875
0.1746741086244583
0.33189886808395386
0.1155870258808136
0.3096879629846001
0.7724081666033108
0.7162094473752455

0.11322850654055751
0.10847180733221087
0.15251432724222921
교육방법별 건수 : 교차표
col_0  count
방법1       26
방법2       28
방법3       24
교육방법별 만족여부 건수 : 교차표
     만족  불만족
방법1   9   17
방법2  10   18
방법3   8   16
            df        sum_sq     mean_sq         F    PR(>F)
method     1.0     27.980888   27.980888  0.122228  0.727597
Residual  76.0  17398.134497  228.922822       NaN       NaN
---------
                          sum_sq    df         F   PR(>F)
C(method + survey)    105.598291   3.0  0.150386  0.92913
Residual            17320.517094  74.0       NaN      NaN
사후검정 : 그룹 전체의 평균에 차이여부를 알려주나, 각 그룹 사이에 평균의 차이는 알려주지 않는다. 그래서 사후검정을 수행한다.
Multiple Comparison of Means - Tukey HSD, FWER=0.05 
====================================================
group1 group2 meandiff p-adj   lower   upper  reject
----------------------------------------------------
     1      2   0.9725 0.9702 -8.9458 10.8909  False
     1      3   1.4904 0.9363 -8.8183  11.799  False
     2      3   0.5179 0.9918 -9.6125 10.6483  False
----------------------------------------------------

사후검정 : 그룹 전체의 평균에 차이여부를 알려주나, 각 그룹 사이에 평균의 차이는 알려주지 않는다. 그래서 사후검정을 수행한다.

 

이상치 제거 함수 참고, 자료 하나의 정규성 확인, 두 개의 정규성 확인 참고

 

 

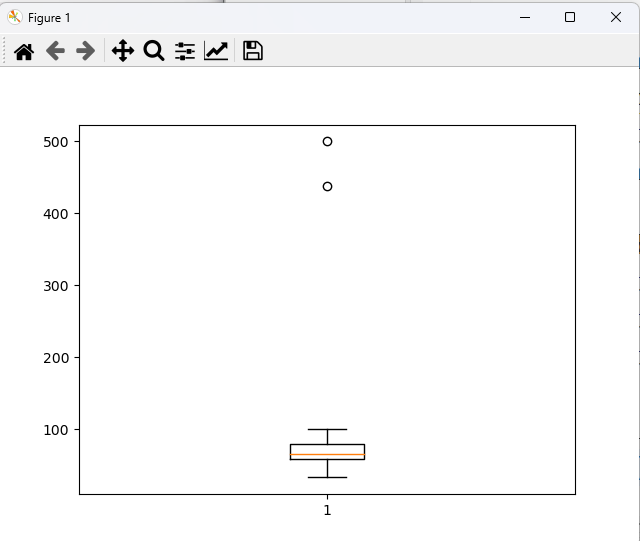
data boxplot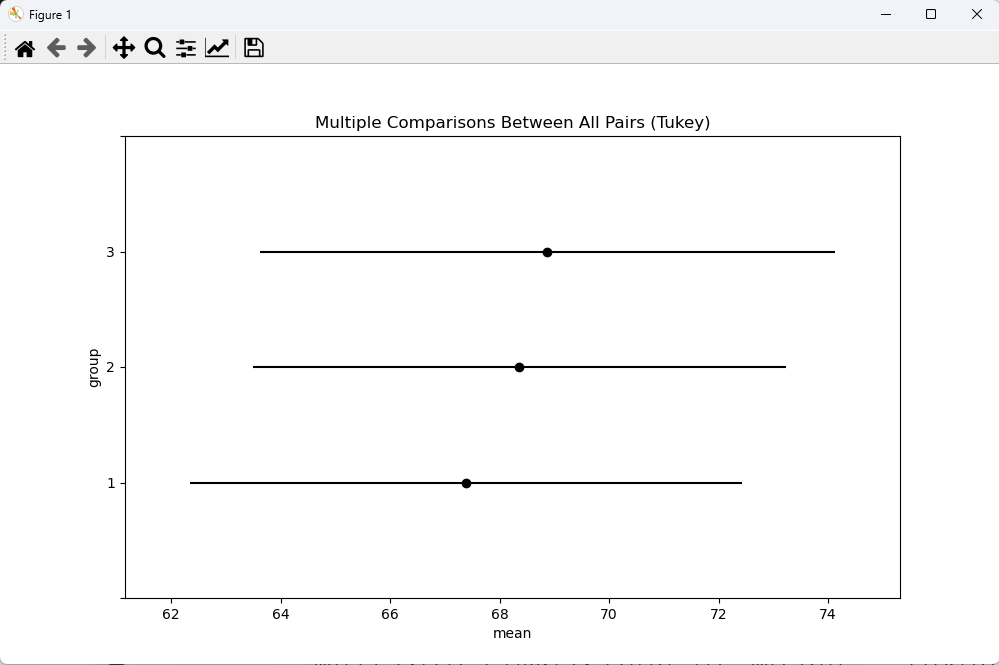

 

사후검정 그래프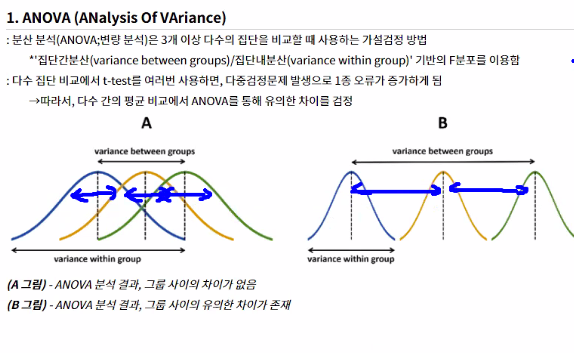

 

집단 내 분산 값은 작아야되고, 집단 간 분산값은 커야 된다.

f  분값을 구해서 귀무 채택, 기각을 검정할 수 있다.