TensorFlow 기초 11 - 단순선형회귀모델 작성 : 방법 3가지(다중 입출력 모델)

 

 

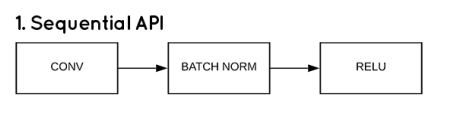
<방법1>

# 단순선형회귀모델 작성 : 방법 3가지 경험하기
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras import optimizers
import numpy as np

# 공부 시간에 따른 성적 결과
x_data = np.array([1,2,3,4,5], dtype=np.float32)
y_data = np.array([5, 32, 55, 61, 80], dtype=np.float32)
print('r =', np.corrcoef(x_data, y_data)) # 0.979

print('방법1 : Sequential api 사용 : 가장 단순하다. 레이어에 노드를 순서대로 쌓아올린 완전 연결층')
model = Sequential()
model.add(Dense(units=1, input_dim=1, activation='linear'))
print(model.summary())

opti = optimizers.Adam(learning_rate=0.1)
model.compile(optimizer=opti, loss='mse', metrics=['mse'])

history = model.fit(x_data, y_data, batch_size=1, epochs=100, verbose=0)
loss_metrics = model.evaluate(x_data, y_data)
print('loss_metrics :', loss_metrics)

from sklearn.metrics import r2_score
print('설명력 :', r2_score(y_data, model.predict(x_data)))
print('실제값 :', y_data)
print('예측값 :', model.predict(x_data).flatten())

new_data = [1.5, 2.3, 5.7]
print('성적 예측값 :', model.predict(new_data).flatten())

# loss(mse) 시각화
import matplotlib.pyplot as plt
plt.rc('font', family='malgun gothic')

plt.plot(history.history['mse'], label='평균제곱오차')
plt.xlabel('학습횟수')
plt.show()

plt.plot(x_data, model.predict(x_data), 'b', x_data, y_data, 'ko')
plt.show()


<console>
r = [[1.         0.97985523]
 [0.97985523 1.        ]]
방법1 : Sequential api 사용 : 가장 단순하다. 레이어에 노드를 순서대로 쌓아올린 완전 연결층
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 1)                 2         
                                                                 
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________
None

1/1 [==============================] - ETA: 0s - loss: 86.8980 - mse: 86.8980
1/1 [==============================] - 0s 103ms/step - loss: 86.8980 - mse: 86.8980
loss_metrics : [86.89796447753906, 86.89796447753906]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 52ms/step
설명력 : 0.8698040858254579
실제값 : [ 5. 32. 55. 61. 80.]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 13ms/step
예측값 : [23.679031 36.374233 49.069435 61.764637 74.45984 ]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 26ms/step
성적 예측값 : [30.02663  40.182793 83.34647 ]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 16ms/step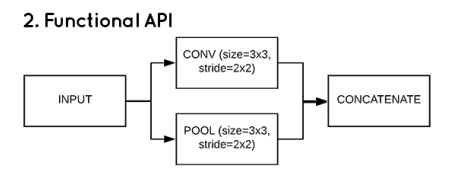

 

 

 

<방법2>

print('방법2 : functional api 사용 : Sequential 보다는 유연한 구조. 입력 데이터로 여러 층을 공유하거나 다양한 종류의 입출력 가능')
from keras.layers import Input
from keras.models import Model
# 각 층은 일종의 함수처럼 처리한다.
inputs = Input(shape=(1,)) # shape의 경우 튜플 타입으로 들어가야 된다.
# outputs = Dense(units=1, activation='linear')(inputs) # 이전 층을 다음 층 함수의 입력으로 사용하도록 변수에 할당
output1 = Dense(units=2, activation='linear')(inputs)
outputs = Dense(units=1, activation='linear')(output1)
model2 = Model(inputs, outputs)

# 이하는 방법 1과 동일
opti = optimizers.Adam(learning_rate=0.1)
model2.compile(optimizer=opti, loss='mse', metrics=['mse'])
model2.fit(x_data, y_data, batch_size=1, epochs=100, verbose=0)
loss_metrics = model2.evaluate(x_data, y_data)
print('loss_metrics :', loss_metrics)
print('설명력 :', r2_score(y_data, model2.predict(x_data)))


<console>
방법2 : functional api 사용 : Sequential 보다는 유연한 구조. 입력 데이터로 여러 층을 공유하거나 다양한 종류의 입출력 가능

1/1 [==============================] - ETA: 0s - loss: 26.7196 - mse: 26.7196
1/1 [==============================] - 0s 107ms/step - loss: 26.7196 - mse: 26.7196
loss_metrics : [26.71963882446289, 26.71963882446289]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 38ms/step
설명력 : 0.9599669803604081

방법 1과는 설계도만 다르다.

 

 

<방법3>

print('\n방법3 : sub classing 사용 : 동적인 구조가 필요한 경우. 메소드를 통해 분석가의 생각을 프로그래밍화')
x_data = np.array([[1],[2],[3],[4],[5]], dtype=np.float32) # 2차원
y_data = np.array([5, 32, 55, 61, 80], dtype=np.float32)

class MyModel(Model):
    def __init__(self): # Model 을 상속받아 생성자를 생성한다.
        super(MyModel, self).__init__()
        # 생성자 내에서 필요한 layer를 생성한 후 call 메소드에서 수행하려는 연산을 적어준다.
        self.d1 = Dense(units=2, activation='linear')
        self.d2 = Dense(units=1, activation='linear')

    def call(self, x):
        inputs = self.d1(x)
        return self.d2(inputs)

model3 = MyModel()

# 이하는 방법 1과 동일
opti = optimizers.Adam(learning_rate=0.1)
model3.compile(optimizer=opti, loss='mse', metrics=['mse'])
model3.fit(x_data, y_data, batch_size=1, epochs=100, verbose=0)
loss_metrics = model3.evaluate(x_data, y_data)
print('loss_metrics :', loss_metrics)
print('설명력 :', r2_score(y_data, model3.predict(x_data)))


<console>
방법3 : sub classing 사용 : 동적인 구조가 필요한 경우. 메소드를 통해 분석가의 생각을 프로그래밍화

1/1 [==============================] - ETA: 0s - loss: 28.5550 - mse: 28.5550
1/1 [==============================] - 0s 90ms/step - loss: 28.5550 - mse: 28.5550
loss_metrics : [28.555017471313477, 28.555017471313477]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 40ms/step
설명력 : 0.9572170998846203

Model class를 상속받아 class를 생성하여 작업하였다.

 

 

<방법3-1>

print('\n방법3-1 : sub classing 사용 : 동적인 구조가 필요한 경우. 메소드를 통해 분석가의 생각을 프로그래밍화')
from keras.layers import Layer

# Custom Layer 작성 : 케라스의 정의된 레이어 이외에 새로운 연산을 위한 레이어 혹은 편의를 목적으로 여러 레이어를 하나로 묶어 처리할 경우
class Linear(Layer):
    def __init__(self, units=1):
        super(Linear, self).__init__()
        self.units = units
        
    def build(self, input_shape): # input_shape[-1] 을 부여하면 알아서 찾아준다.
        self.w = self.add_weight(shape=(input_shape[-1], self.units),
                                 initializer = 'random_normal', trainable=True)
        # 모델의 가중치, 편향과 관련된 내용을 기술(build)
        
        self.b = self.add_weight(shape=(self.units,), initializer = 'zeros', trainable=True)
        
    def call(self, inputs): # 정의된 값들을 이용하여 해당 층의 로직을 기술
        # y = wx + b, matmul()은 행렬곱이다.
        return tf.matmul(inputs, self.w) + self.b
    
class MLP(Model):
    def __init__(self):
        super(MLP, self).__init__()
        # self.linear1 = Linear(1) Layer 가 1개일 때
        self.linear1 = Linear(2)
        self.linear2 = Linear(1)
        
    def call(self, inputs):
        # return self.linear1(inputs) Layer 가 1개일 때
        net = self.linear1(inputs)
        return self.linear2(net)
    
model4 = MLP()

# 이하는 방법 1과 동일
opti = optimizers.Adam(learning_rate=0.1)
model4.compile(optimizer=opti, loss='mse', metrics=['mse'])
model4.fit(x_data, y_data, batch_size=1, epochs=100, verbose=0)
loss_metrics = model4.evaluate(x_data, y_data)
print('loss_metrics :', loss_metrics)
print('설명력 :', r2_score(y_data, model4.predict(x_data)))
print(model4.summary())


<console>
방법3-1 : sub classing 사용 : 동적인 구조가 필요한 경우. 메소드를 통해 분석가의 생각을 프로그래밍화

1/1 [==============================] - ETA: 0s - loss: 26.6499 - mse: 26.6499
1/1 [==============================] - 0s 87ms/step - loss: 26.6499 - mse: 26.6499
loss_metrics : [26.649927139282227, 26.649927139282227]

1/1 [==============================] - ETA: 0s
1/1 [==============================] - 0s 37ms/step
설명력 : 0.9600714295910588
Model: "mlp"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 linear (Linear)             multiple                  4         
                                                                 
 linear_1 (Linear)           multiple                  3         
                                                                 
=================================================================
Total params: 7
Trainable params: 7
Non-trainable params: 0
_________________________________________________________________
None

Layer class를 상속받아 class 생성하였다.

 

 

평균제곱오차

loss가 60 이상부터는 잔잔하기 때문에 학습은 60번 정도로 해도 된다.

 

예측값, 실제값 시각화(추세선)