다중회귀모델 예제(degree)

 

 

# 회귀분석 : 선형회귀, 다항회귀
import pandas as pd
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt
plt.rc('font', family = 'malgun gothic')

df = pd.read_csv('../testdata/housing.data', header = None, sep = '\s+') # sep = 공백으로 구분
df.columns = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
print(df.head(3), df.shape) # (506, 14)

print(df.corr()) # 상관관계 호출

x = df[['LSTAT']].values # metrics 로 넣어준다.
print(x[:3])
y = df['MEDV'].values
print(y[:3])

model = LinearRegression()

# 단순회귀
model.fit(x, y)

x_fit = np.arange(x.min(), x.max(), 1)[:, np.newaxis] # 1은 1차원을 의미
# print(x_fit)
y_lin_fit = model.predict(x_fit) # 그래프 표시용
# print(y_lin_fit)

model_r2 = r2_score(y, model.predict(x))
print('model_r2 :', model_r2)

# 다항회귀
quad = PolynomialFeatures(degree = 2) # 2열 추가
cubic = PolynomialFeatures(degree = 3)
x_quad = quad.fit_transform(x)
x_cubic = cubic.fit_transform(x)

# degree = 2
model.fit(x_quad, y)
y_quad_fit = model.predict(quad.fit_transform(x_fit)) # 그래프 표시용
q_r2 = r2_score(y, model.predict(x_quad))
print('q_r2 :',q_r2)

# degree = 3
model.fit(x_cubic, y)
y_cubic_fit = model.predict(cubic.fit_transform(x_fit)) # 그래프 표시용
c_r2 = r2_score(y, model.predict(x_cubic))
print('c_r2 :',c_r2)

# 시각화
plt.scatter(x, y, c = 'lightgray', label = '학습 데이터')
plt.plot(x_fit, y_lin_fit, linestyle = ':', label = 'linear fit(d=1), $R^2=%.2f$'%model_r2, c='b', lw=3)
plt.plot(x_fit, y_quad_fit, linestyle = '-', label = 'quad fit(d=2), $R^2=%.2f$'%q_r2, c='r', lw=3)
plt.plot(x_fit, y_cubic_fit, linestyle = '--', label = 'cubic fit(d=3), $R^2=%.2f$'%c_r2, c='k', lw=3)
plt.xlabel('하위계층비율')
plt.ylabel('주택가격')
plt.legend() # label을 적었으면 legend 함수로 호출해야 적용된다.
plt.show()


<console>
      CRIM    ZN  INDUS  CHAS    NOX  ...    TAX  PTRATIO       B  LSTAT  MEDV
0  0.00632  18.0   2.31     0  0.538  ...  296.0     15.3  396.90   4.98  24.0
1  0.02731   0.0   7.07     0  0.469  ...  242.0     17.8  396.90   9.14  21.6
2  0.02729   0.0   7.07     0  0.469  ...  242.0     17.8  392.83   4.03  34.7

[3 rows x 14 columns] (506, 14)
             CRIM        ZN     INDUS  ...         B     LSTAT      MEDV
CRIM     1.000000 -0.200469  0.406583  ... -0.385064  0.455621 -0.388305
ZN      -0.200469  1.000000 -0.533828  ...  0.175520 -0.412995  0.360445
INDUS    0.406583 -0.533828  1.000000  ... -0.356977  0.603800 -0.483725
CHAS    -0.055892 -0.042697  0.062938  ...  0.048788 -0.053929  0.175260
NOX      0.420972 -0.516604  0.763651  ... -0.380051  0.590879 -0.427321
RM      -0.219247  0.311991 -0.391676  ...  0.128069 -0.613808  0.695360
AGE      0.352734 -0.569537  0.644779  ... -0.273534  0.602339 -0.376955
DIS     -0.379670  0.664408 -0.708027  ...  0.291512 -0.496996  0.249929
RAD      0.625505 -0.311948  0.595129  ... -0.444413  0.488676 -0.381626
TAX      0.582764 -0.314563  0.720760  ... -0.441808  0.543993 -0.468536
PTRATIO  0.289946 -0.391679  0.383248  ... -0.177383  0.374044 -0.507787
B       -0.385064  0.175520 -0.356977  ...  1.000000 -0.366087  0.333461
LSTAT    0.455621 -0.412995  0.603800  ... -0.366087  1.000000 -0.737663
MEDV    -0.388305  0.360445 -0.483725  ...  0.333461 -0.737663  1.000000

[14 rows x 14 columns]
[[4.98]
 [9.14]
 [4.03]]
[24.  21.6 34.7]
model_r2 : 0.5441462975864799
q_r2 : 0.6407168971636611
c_r2 : 0.6578476405895719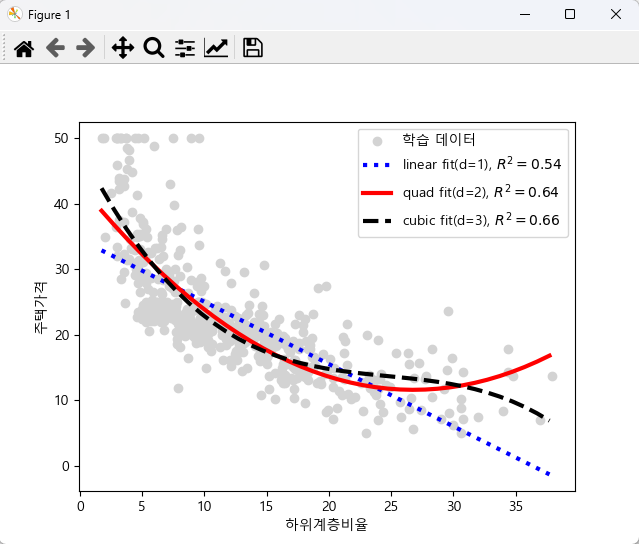

 

 

선형으로도 만들어보고 다항회귀모델로도 적용시켜보았다. degree(열 추가)가 2개일 때와 3개일 때이다.

어떠한 데이터에 어떠한 것을 쓸 것인가는 데이터 사이언티스트에 역량에 달렸다.