Python 데이터분석 기초 34 - 서로 독립인 두 집단의 평균 차이 검정(independent samples t-test), 정규성, 등분산성

 

 

예제 1)

# 두 집단의 가설검정 – 실습 시 분산을 알지 못하는 것으로 한정하겠다.
# * 서로 독립인 두 집단의 평균 차이 검정(independent samples t-test)
# 남녀의 성적, A반과 B반의 키, 경기도와 충청도의 소득 따위의 서로 독립인 두 집단에서 얻은 표본을 독립표본(two sample)이라고 한다.

from scipy import stats
import pandas as pd
from numpy import average

# 실습) 남녀 두 집단 간 파이썬 시험의 평균 차이 검정
male = [75, 85, 100, 72.5, 86.5]
female = [63.2, 76, 52, 100, 70]

# 귀무 : 남녀 두 집단 간 파이썬 시험의 평균에 차이가 없다.
# 대립 : 남녀 두 집단 간 파이썬 시험의 평균에 차이가 있다.

print(average(male), ' ', average(female)) # 83.8   72.24
print(83.8 - 72.24) # 11.560

two_sample = stats.ttest_ind(male, female) # 두 개의 표본에 대한 t-test 실시
print(two_sample)
# Ttest_indResult(statistic=1.233193127514512, pvalue=0.2525076844853278)
# 해석 : pvalue = 0.25250768 > 0.05 이므로 귀무가설 채택


<console>
83.8   72.24
11.560000000000002
Ttest_indResult(statistic=1.233193127514512, pvalue=0.2525076844853278)

 

예제 2)

# 실습) 두 가지 교육방법에 따른 평균시험 점수에 대한 검정 수행 two_sample.csv'
data = pd.read_csv("../testdata/two_sample.csv")
print(data.head(3), len(data))

# 귀무 : 두 가지 교육방법에 따른 평균시험 점수에 차이가 없다.
# 대립 : 두 가지 교육방법에 따른 평균시험 점수에 차이가 있다.

ms = data[['method', 'score']]
print(ms)
# 교육방법별로 데이터 분리
m1 = ms[ms['method'] == 1]
m2 = ms[ms['method'] == 2]

score1 = m1['score']
score2 = m2['score']
print(score1)
print(score2)
print(score1.isnull().sum()) # 0
print(score2.isnull().sum()) # 2 NaN : 제거, 0, 평균으로 대체

sco1 = score1.fillna(score1.mean()) 
sco2 = score2.fillna(score2.mean()) # NaN를 평균으로 대체
print(sco2.isnull().sum())

# 정규성 검정
import matplotlib.pyplot as plt
import seaborn as sns
# sns.histplot(sco1, kde=True, color='r')
# sns.histplot(sco2, kde=True, color='b')
# plt.show()

# 정규성
print(stats.shapiro(sco1).pvalue) # 0.3679903745651245 > 0.05 정규성 만족
print(stats.shapiro(sco2).pvalue) # 0.6714189648628235 > 0.05 정규성 만족

# 등분산성
print(stats.levene(sco1, sco2).pvalue)   # 0.4568427112977609 > 0.05 등분산성 만족, 표본이 30개 이상일 경우 사용(모수 검정)
print(stats.fligner(sco1, sco2).pvalue)  # 0.44323735267062647 > 0.05 등분산성 만족, 표본이 30개 이상일 경우 사용(모수 검정)
print(stats.bartlett(sco1, sco2).pvalue) # 0.26789717886602216 > 0.05 등분산성 만족, 표본이 30개 미만일 경우 사용(비모수 검정)

result = stats.ttest_ind(sco1, sco2) # 정규성 만족, 등분산성 만족
print('t-value:%.5f, p-value:%.5f'%result) # t-value:-0.19649, p-value:0.84505
# 해석 : p-value : 0.86309 > 0.05 이므로 귀무 채택. 두 가지 교육방법에 따른 평균시험 점수에 차이가 없다.

print('참고 ---------')
result = stats.ttest_ind(sco1, sco2, equal_var=True) # 정규성 만족, 등분산성 만족
print('t-value:%.5f, p-value:%.5f'%result)

result = stats.ttest_ind(sco1, sco2, equal_var=False) # 정규성 만족, 등분산성 불만족
print('t-value:%.5f, p-value:%.5f'%result)

# result2 = stats.wilcoxon(sco1, sco2) # 정규성을 만족하지 않는 경우 # ValueError: The samples x and y must have the same length.
result2 = stats.mannwhitneyu(sco1, sco2)
print('t-value:%.5f, p-value:%.5f'%result2)


<console>
   no  gender  method  survey  score
0   1       1       1       1    5.1
1   2       1       2       0    NaN
2   3       1       1       1    4.7 50
    method  score
0        1    5.1
1        2    NaN
2        1    4.7
3        2    NaN
4        1    5.4
5        2    4.4
6        2    4.9
7        1    5.2
8        2    4.3
9        2    5.8
10       1    5.7
11       2    5.1
12       2    5.3
13       2    5.4
14       1    5.1
15       1    4.8
16       1    4.1
17       1    4.8
18       1    5.2
19       1    4.7
20       1    4.4
21       1    5.2
22       1    5.3
23       1    6.1
24       1    6.3
25       1    4.1
26       1    5.3
27       1    5.1
28       1    3.8
29       1    5.6
30       1    5.3
31       1    6.4
32       1    5.5
33       1    4.7
34       2    3.9
35       2    3.3
36       2    5.6
37       1    5.6
38       1    6.2
39       1    5.9
40       1    3.4
41       2    6.3
42       1    6.4
43       2    6.8
44       1    5.2
45       2    5.5
46       1    5.8
47       2    5.4
48       2    6.7
49       1    5.2
0     5.1
2     4.7
4     5.4
7     5.2
10    5.7
14    5.1
15    4.8
16    4.1
17    4.8
18    5.2
19    4.7
20    4.4
21    5.2
22    5.3
23    6.1
24    6.3
25    4.1
26    5.3
27    5.1
28    3.8
29    5.6
30    5.3
31    6.4
32    5.5
33    4.7
37    5.6
38    6.2
39    5.9
40    3.4
42    6.4
44    5.2
46    5.8
49    5.2
Name: score, dtype: float64
1     NaN
3     NaN
5     4.4
6     4.9
8     4.3
9     5.8
11    5.1
12    5.3
13    5.4
34    3.9
35    3.3
36    5.6
41    6.3
43    6.8
45    5.5
47    5.4
48    6.7
Name: score, dtype: float64
0
2
0
0.3679903745651245
0.6714189648628235
0.4568427112977609
0.44323735267062647
0.26789717886602216
t-value:-0.19649, p-value:0.84505
참고 ---------
t-value:-0.19649, p-value:0.84505
t-value:-0.18204, p-value:0.85693
t-value:261.00000, p-value:0.69678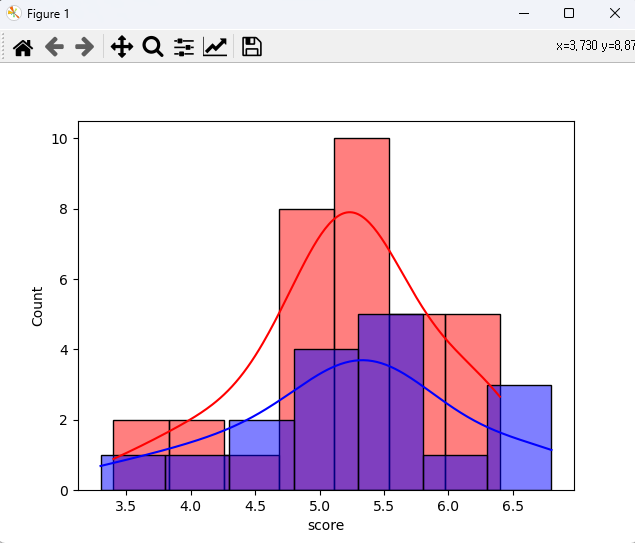

 

문제 2번 정규성 검사

 

 

등분산성 : 등분산성 조건을 충족하는지 확인하기 위해서는 scipy에서 제공하는 검정을 주로 사용한다.

                 하지만 등분산성 조건을 충족하지 못하더라도 t-test를 사용할 수 있기는 하다. 

 

 - bartlett : scipy.stats.bartlett

 - fligner : scipy.stats.fligner

 - levene : scipy.stats.levene

 

등분산성은 집단 간의 비교를 할때만 검정한다.

 

 

참고

Daum 카페