Python 데이터분석 기초 29 - # 가설검정 중 카이제곱(교차분석) 대립 가설 세워보기, 카이제곱이란?

 

# 가설검정 중 카이제곱(교차분석)
# 범주형 하나 또는 두 개의 변수 간의 상관관계를 측정
# 카이제곱 분포는 데이터의 분산이 퍼져있는 모습을 분포로 만든 것이다.
# x² = sum((실제값 -기대값)² / 기대값)
# 기대값 = 각행의 주변합 * 각열의 주변합 / 총합(전체표본수)
#      = (행의 합/전체표본수 * 열의합/전체표본수) * 전체 표본수

# 가정
# 귀무 가설 : 벼락치기 공부는 합격여부와 관련이 없다(독립적).    - 정설 -
# 대립 가설 : 벼락치기 공부는 합격여부와 관련이 있다(비독립적).   - 대립 -

import pandas as pd
data = pd.read_csv('../testdata/pass_cross.csv', encoding='euc-kr') # utf-8이 안되면 euc-kr로 하기!
print(data.head(3))
print(data.shape[0]) # 행의 갯수 50개
print(data.shape[1]) # 열의 갯수 4개
print()
print(data[(data['공부함'] == 1) & (data['합격'] == 1)].shape[0]) # 18행
print(data[(data['공부함'] == 1) & (data['불합격'] == 1)].shape[0]) # 7행

print()
ctab = pd.crosstab(index = data['공부안함'], columns = data['불합격'], margins= True) # margins 는 합 갯수가 나온다.
ctab.columns = ['합격','불합격', '행합']  # 행 이름 변경
ctab.index = ['공부함', '공부안함', '열합'] # 열 이름 변경
print(ctab)
print(25 * 30 / 50) # 기대값 얻는 수식
print(25 * 20 / 50)

# 판정 방법1 : 카이제곱표를 이용
chi2 = (18 - 15)**2 / 15 + (7 - 10)**2 / 10 + (12 - 15)**2 / 15 + (13 - 10)**2 / 10
print('카이제곱 :', chi2)

print('-------자유도-------')
# 자유도(행의 갯수 - 1) * (열의 갯수 - 1) : 1
# 카이제곱표를 이용해 임계값(criticla value) 얻기 : 3.84
# 판정 : x²(카이제곱) 값이 cv 값 왼쪽에 있으므로 귀무가설 채택
# 즉, 벼락치기 공부는 합격여부와 관련이 없다(독립적).

# 판정 방법2 : p-value를 이용
import scipy.stats as stats

chi2, p, _, _ = stats.chi2_contingency(ctab) # p-value 값 구하기, 
print('chi2:{}, p:{}'.format(chi2, p)) # chi2:3.0, p:0.5578254003710748
# 판정 : p(유의확률):0.557825 > α(유의수준) 0.05 이므로 귀무가설 채택(대립가설 기각)
# 즉, 벼락치기 공부는 합격여부와 관련이 없다(독립적). 검정에 사용된 샘플 데이터는 우연히 발생된 데이터이다.



<console>
   공부함  공부안함  합격  불합격
0    1     0   1    0
1    1     0   1    0
2    0     1   0    1
50
4

18
7

      합격  불합격  행합
공부함   18    7  25
공부안함  12   13  25
열합    30   20  50
15.0
10.0
카이제곱 : 3.0
-------자유도-------
chi2:3.0, p:0.5578254003710748

 

 

카이제곱표

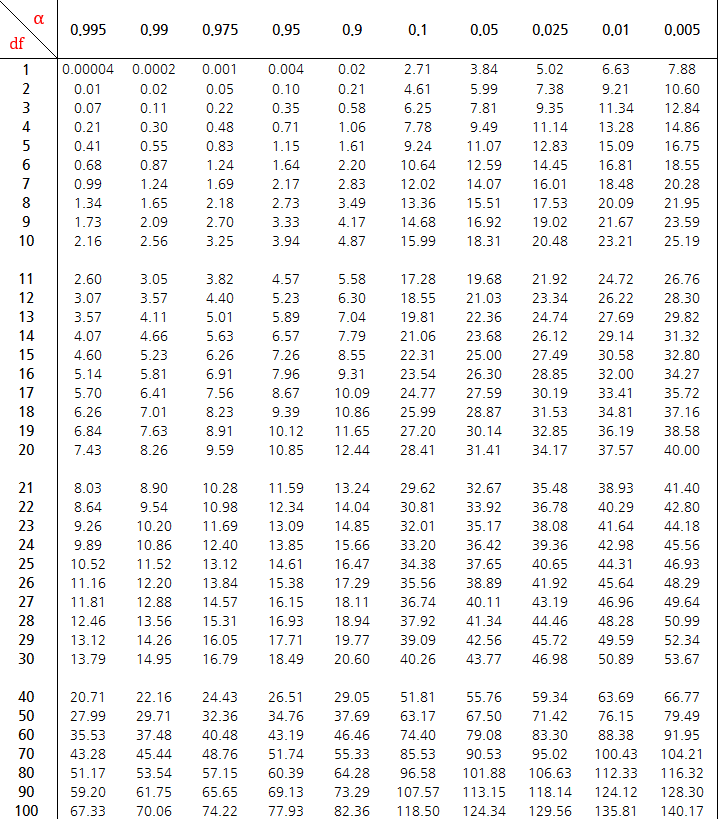
출저 : https://math100.tistory.com/45

 

 

카이제곱이란?

[딥러닝] 카이제곱