Python 데이터 분석
회귀분석모형의 적절성을 위한 5가지 조건 예제
코딩탕탕
2022. 11. 16. 12:31
# 회귀분석 문제 3)
# kaggle.com에서 carseats.csv 파일을 다운 받아 (https://github.com/pykwon 에도 있음)
# Sales 변수에 영향을 주는 변수들을 선택하여 선형회귀분석을 실시한다.
# 변수 선택은 모델.summary() 함수를 활용하여 타당한 변수만 임의적으로 선택한다.
# 회귀분석모형의 적절성을 위한 조건도 체크하시오.
# 완성된 모델로 Sales를 예측.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api
plt.rc('font', family = 'malgun gothic')
import seaborn as sns
import statsmodels.formula.api as smf
df = pd.read_csv('../testdata/Carseats.csv')
print(df.head(2))
print(df.info())
df = df.drop([df.columns[6], df.columns[9], df.columns[10]], axis = 1) # 6, 9, 10 열은 제외.
print(df.head(2))
print(df.corr()) # 상관관계 확인
lm = smf.ols(formula = 'Sales ~ Income + Advertising + Price + Age', data = df).fit()
print('요약 결과: \n', lm.summary()) # p-value : 1.33e-38 < 0.05 이므로 유의한 데이터이다.
df_lm = df.iloc[:,[0, 2, 3, 5, 6]]
print(df_lm)
print('---회귀분석모형의 적절성 확인 작업')
# 잔차 구하기
fitted = lm.predict(df_lm) # 예측값
residual = df_lm['Sales'] - fitted # 실제값 - 예측값
print(residual[:3])
print('잔차의 평균 :', np.mean(residual)) # -8.057998712729386e-15
print('--- 선형성 ---')
sns.regplot(fitted, residual, lowess = True, line_kws = {'color':'red'})
plt.plot([fitted.min(), fitted.max()], [0, 0], '--', c = 'b')
plt.show() # 잔차가 일정하게 분포되어 있으므로 선형성 만족
print('--- 정규성 ---')
import scipy.stats as stats
sr = stats.zscore(residual)
(x, y), _ = stats.probplot(sr)
sns.scatterplot(x, y)
plt.plot([-3, 3], [-3, 3], '--', c = 'b')
plt.show() # 잔차항이 정규분포를 따름
print('shapiro test :', stats.shapiro(residual)) # p-value : 0.2127407342195511 > 0.05 이므로 정규성 만족
print('--- 독립성 ---')
# Durbin-Watson : 1.931 2에 근사하므로 독립성 만족
print('--- 등분산성 ---')
sr = stats.zscore(residual)
sns.regplot(fitted, np.sqrt(abs(sr)), lowess = True, line_kws = {'color':'red'})
plt.show() # 평균선을 기준으로 일정한 패턴을 보이지 않아 등분산성 만족.
print('--- 다중공선성 ---')
from statsmodels.stats.outliers_influence import variance_inflation_factor
df2 = df[['Income', 'Advertising', 'Price', 'Age']]
print(df2.head(2))
print(df2.shape) # (400, 4)
vifdf = pd.DataFrame()
vifdf['vif_value'] = [variance_inflation_factor(df2.values, i) for i in range(df2.shape[1])]
print(vifdf) # 모든 변수가 10을 넘기지 않음. 다중공선성 우려 없음.
# 모델 저장
import joblib
joblib.dump(lm, 'yhs.model') # yhs.model 이름으로 저장
del lm # 이 페이지에서 삭제
print('-----지금부터는 저장된 모델을 읽어 사용함------')
lm = joblib.load('yhs.model')
# print(lm_dajung.summary())
# 완성된 모델로 새로운 독립변수의 값을 주고 Sales를 예측
new_df = pd.DataFrame({'Income':[33, 55, 66], 'Advertising':[10, 13, 16],
'Price':[100, 120, 140], 'Age':[33, 35, 40]})
pred = lm.predict(new_df)
print('Sales에 대한 예측 결과 : \n', pred)
<console>
Sales CompPrice Income Advertising ... Age Education Urban US
0 9.50 138 73 11 ... 42 17 Yes Yes
1 11.22 111 48 16 ... 65 10 Yes Yes
[2 rows x 11 columns]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 400 entries, 0 to 399
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Sales 400 non-null float64
1 CompPrice 400 non-null int64
2 Income 400 non-null int64
3 Advertising 400 non-null int64
4 Population 400 non-null int64
5 Price 400 non-null int64
6 ShelveLoc 400 non-null object
7 Age 400 non-null int64
8 Education 400 non-null int64
9 Urban 400 non-null object
10 US 400 non-null object
dtypes: float64(1), int64(7), object(3)
memory usage: 34.5+ KB
None
Sales CompPrice Income Advertising Population Price Age Education
0 9.50 138 73 11 276 120 42 17
1 11.22 111 48 16 260 83 65 10
Sales CompPrice Income ... Price Age Education
Sales 1.000000 0.064079 0.151951 ... -0.444951 -0.231815 -0.051955
CompPrice 0.064079 1.000000 -0.080653 ... 0.584848 -0.100239 0.025197
Income 0.151951 -0.080653 1.000000 ... -0.056698 -0.004670 -0.056855
Advertising 0.269507 -0.024199 0.058995 ... 0.044537 -0.004557 -0.033594
Population 0.050471 -0.094707 -0.007877 ... -0.012144 -0.042663 -0.106378
Price -0.444951 0.584848 -0.056698 ... 1.000000 -0.102177 0.011747
Age -0.231815 -0.100239 -0.004670 ... -0.102177 1.000000 0.006488
Education -0.051955 0.025197 -0.056855 ... 0.011747 0.006488 1.000000
[8 rows x 8 columns]
요약 결과:
OLS Regression Results
==============================================================================
Dep. Variable: Sales R-squared: 0.371
Model: OLS Adj. R-squared: 0.364
Method: Least Squares F-statistic: 58.21
Date: Wed, 16 Nov 2022 Prob (F-statistic): 1.33e-38
Time: 12:27:19 Log-Likelihood: -889.67
No. Observations: 400 AIC: 1789.
Df Residuals: 395 BIC: 1809.
Df Model: 4
Covariance Type: nonrobust
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 15.1829 0.777 19.542 0.000 13.656 16.710
Income 0.0108 0.004 2.664 0.008 0.003 0.019
Advertising 0.1203 0.017 7.078 0.000 0.087 0.154
Price -0.0573 0.005 -11.932 0.000 -0.067 -0.048
Age -0.0486 0.007 -6.956 0.000 -0.062 -0.035
==============================================================================
Omnibus: 3.285 Durbin-Watson: 1.931
Prob(Omnibus): 0.194 Jarque-Bera (JB): 3.336
Skew: 0.218 Prob(JB): 0.189
Kurtosis: 2.903 Cond. No. 1.01e+03
==============================================================================
Sales Income Advertising Price Age
0 9.50 73 11 120 42
1 11.22 48 16 83 65
2 10.06 35 10 80 59
3 7.40 100 4 97 55
4 4.15 64 3 128 38
.. ... ... ... ... ...
395 12.57 108 17 128 33
396 6.14 23 3 120 55
397 7.41 26 12 159 40
398 5.94 79 7 95 50
399 9.71 37 0 120 49
[400 rows x 5 columns]
---회귀분석모형의 적절성 확인 작업
0 1.121679
1 1.509747
2 0.747950
dtype: float64
잔차의 평균 : -8.057998712729386e-15
--- 선형성 ---
--- 정규성 ---
shapiro test : ShapiroResult(statistic=0.994922399520874, pvalue=0.2127407342195511)
--- 독립성 ---
--- 등분산성 ---
--- 다중공선성 ---
Income Advertising Price Age
0 73 11 120 42
1 48 16 83 65
(400, 4)
vif_value
0 5.971040
1 1.993726
2 9.979281
3 8.267760
-----지금부터는 저장된 모델을 읽어 사용함------
Sales에 대한 예측 결과 :
0 9.410249
1 8.765653
2 7.856649
dtype: float64
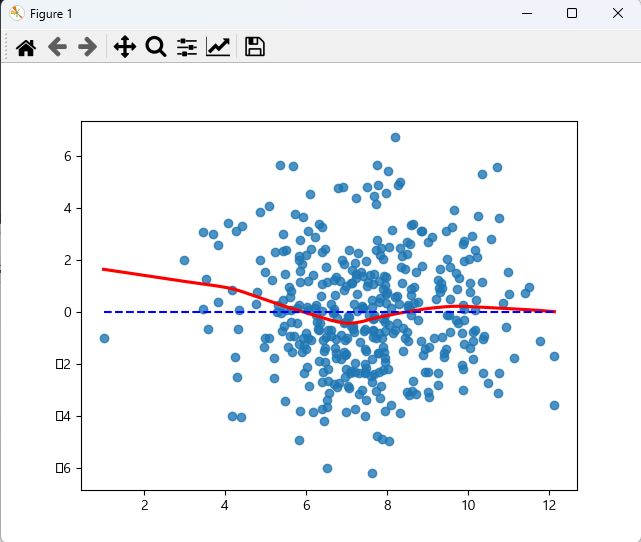
잔차가 일정하게 분포되어 있으므로 선형성 만족
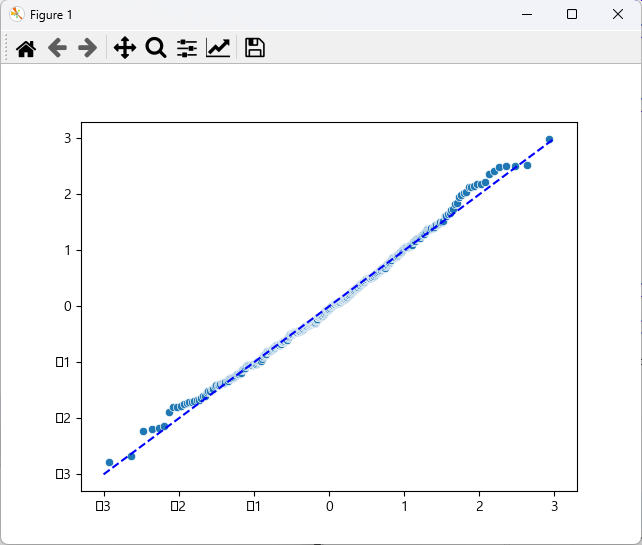
잔차항이 정규분포를 따르므로 정규성 만족

모든 변수가 10을 넘기지 않으므로 다중공선성 우려 없다. 등분산성 만족