R 기초 18 - 통계분석, 기술통계, 표준화, 정규화, 변동계수, 공분산, 상관계수

 

정규화와 표준화 정의 참조

[통계] 정규화(Normalization) vs 표준화(Standardization)

 

# 통계분석 : 어떤 데이터가 주어졌을 때 데이터 간의 관계를 파악하고 이를 분석하는 것

# 기술통계 : 자료를 정리하고 요약 및 시각화를 하는 기초적인 총계
# 중심경향값 (평균, 중위수, 최빈수), 산포도(분산, 표준편차, 범위, 사분위수), 분포도(왜도, 첨도)
# 기초 통계량 계산 함수 약간 보기
mean(1:5)     # 평균
var(1:5)      # 분산
sd(1:5)       # 표준편차
summary(1:10) # 평균, 최빈값, 최댓값 등 호출

# 표준화(Standardization), 정규화(Normalization)
# 표준화 : 평균과 표준편차를 사용하여 평균이 0, 표준편차를 1로 만드는 작업
# 수식 : (요소값 - 평균) / 표준편차

# iris dataset로 작업 진행
head(iris, 3)

df <- iris[, 1:4]
head(df, 3)
dim(df)
# 방법 1 : 수식 직접 사용
(iris$Sepal.Length - mean(iris$Sepal.Length)) / sd(iris$Sepal.Length) # 표준화
df$Sepal.Length

# 방법 2 : 내장 함수 사용
scale(df$Sepal.Length)  # 위의 수식을 함수로 만들어놔서 내장함수를 부르면 된다.
scale(df)

# 방법 3 : 함수작성 후 사용
func1 <- function(x){
  return((x- mean(x)) / sd(x))
}

func1(iris$Sepal.Length)

# 방법 4 : 내장 함수 사용
apply(X=as.matrix(df$Sepal.Length), MARGIN = 2, FUN = "func1")
apply(X=df, MARGIN = 2, FUN = "func1")


# 정규화 : 최대값과 최소값을 사용하여 원래 데이터의 최소값을 0, 최대값을 1로 만드는 작업
# 수식 : (요소값 - 최소값) / (최대값 - 최소값)

func2 <- function(x){
  return((x - min(x)) / (max(x) - min(x)))
}

func2(iris$Sepal.Length)
func2(1:10)
func2(-10:-20)

# 변동계수 : 평균에 대한 표준편차의 비율을 의미한다. 표준편차를 산술평균으로 나눈 값
# 평균이 크게 다른 두 개 이상의 집단이 있을 때, 각 집단의 상대적 동질성을 감안한 산포도의 척도
# 변동계수 = 표준편차 / 평균

# 예) 3개의 샘플에 대해 2명의 관측자가 물 용량을 측정한 데이터가 있다.
tom <- c(54, 50, 52)             # 물 : 리터 단위 측정
james <- c(54017, 49980, 52003)  # 물 : 밀리리터 단위 측정
mean(tom)   # 52
mean(james) # 52000
sd(tom)
sd(james)

sd(tom) / mean(tom)     # 리터 단위 측정한 변동계수
sd(james) / mean(james) # 밀리리터 단위 측정한 변동계수

 

상관계수

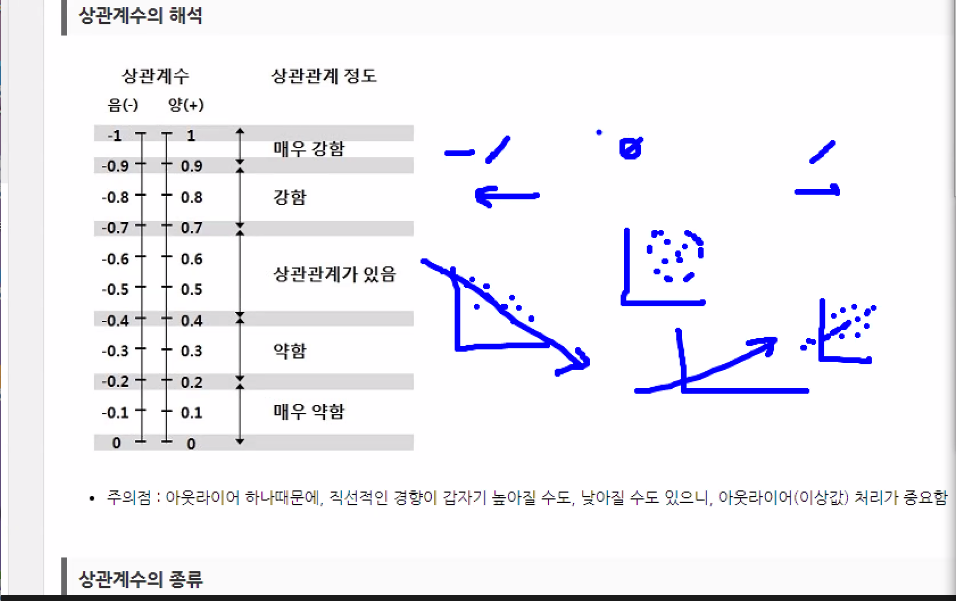
패턴이 우하향하게 되면 -1에 가까워진다.

패턴이 우상향하게 되면 1에 가까워진다.

패턴이 고르게 분포되어있으면 상관관계가 없다고 보고 0이 된다.

 

상관계수가 0.2 보다 적을경우에는 상관계수가 없는 것으로 보고 분석을 하지 않는다.

 

# 상관계수 : 변수들 간의 관련성을 분석. 공분산을 표준화한 값. -1 ~ 0 ~ 1 사이의 값으로 관계를 분석
# 공분산 : 두 개 이상의 확률변수에 대한 관계를 보여주는 값. 힘의 방향은 알 수 있으나 크기는 제각각이다.
plot(1:5, 2:6) # 그래프 출력
cov(1:5, 2:6)  # 2.5이므로 우상향 패턴을 보인다.

plot(1:5, c(3,3,3,3,3))
cov(1:5, c(3,3,3,3,3)) # 0이므로 패턴을 보이지 않는다.

plot(1:5, 5:1)
cov(1:5, 5:1)  # -2.5이므로 우하향 패턴을 보인다.
plot(1:5, c(5000, 4000, 3000, 2000, 1000))
cov(1:5, c(5000, 4000, 3000, 2000, 1000))
cor(1:5, 5:1)  # 표준화를 하여 -1 ~ 1로 나타낸다. -1이므로 완전 상관관계이다.
cor(1:5, c(5000, 4000, 3000, 2000, 1000)) # 이하동문

plot(1:5, c(5000, 3500, 2200, 1000, 1200))
cov(1:5, c(5000, 3500, 2200, 1000, 1200))  # 공분산
cor(1:5, c(5000, 3500, 2200, 1000, 1200))  # 상관계수 -0.9523218 상관관계가 매우 강하다.

 

프랜시스 골턴이 만든 자료를 이용해 예를들어 설명하겠다.

# 상관계수 : 변수들 간의 관련성을 분석. 공분산을 표준화한 값. -1 ~ 0 ~ 1 사이의 값으로 관계를 분석
# 공분산 : 두 개 이상의 확률변수에 대한 관계를 보여주는 값. 힘의 방향은 알 수 있으나 크기는 제각각이다.
plot(1:5, 2:6) # 그래프 출력
cov(1:5, 2:6)  # 2.5이므로 우상향 패턴을 보인다.

plot(1:5, c(3,3,3,3,3))
cov(1:5, c(3,3,3,3,3)) # 0이므로 패턴을 보이지 않는다.

plot(1:5, 5:1)
cov(1:5, 5:1)  # -2.5이므로 우하향 패턴을 보인다.
plot(1:5, c(5000, 4000, 3000, 2000, 1000))
cov(1:5, c(5000, 4000, 3000, 2000, 1000))
cor(1:5, 5:1)  # 표준화를 하여 -1 ~ 1로 나타낸다. -1이므로 완전 상관관계이다.
cor(1:5, c(5000, 4000, 3000, 2000, 1000)) # 이하동문

plot(1:5, c(5000, 3500, 2200, 1000, 1200))
cov(1:5, c(5000, 3500, 2200, 1000, 1200))  # 공분산
cor(1:5, c(5000, 3500, 2200, 1000, 1200))  # 상관계수 -0.9523218 상관관계가 매우 강하다.

# 예제 프랜시스 골턴이 만든 csv 자료를 사용
hf <- read.csv("testdata/galton.csv", header = T)
head(hf, 3)
dim(hf)
str(hf)
summary(hf)

hf_man <- subset(hf, sex=='M') # 조건을 거는 함수 성별이 M인 사람만 호출
hf_man
hf_man <- hf_man[c("father", "height")]
dim(hf_man)
head(hf_man, 3)

# 공분산 : 수식
f_mean <- mean(hf_man$father)
s_mean <- mean(hf_man$height)
cov_sum <- sum((hf_man$father - f_mean) * (hf_man$height - s_mean)) # 편차 곱의 합
cov_xy <- cov_sum / (nrow(hf_man) - 1)
cov_xy   # 2.368441 양의 관계가 있다.

# 공분산 : 함수(추천)
cov(hf_man$father, hf_man$height)  # 2.368441

# 상관계수 : 수식
r_xy <- cov_xy / (sd(hf_man$father) * sd(hf_man$height))
r_xy  # 0.3913174


# 상관계수 : 함수
cor(hf_man$father, hf_man$height)  # 0.3913174

plot(height ~ father, data=hf_man)
abline(lm(height ~ father, data = hf_man), col='red', lwd=2) # 그래프에 평균선의 값을 직선 긋기

# 상관계수 검정 : 상관계수의 통계적 유의성을 판단할 수 있다.
cor.test(hf_man$father, hf_man$height, method = 'pearson')